В первой части «Теории баунти-турниров» мы проанализировали, как структура призовых фондов баунти-турниров закладывает основу для важных отличий между турнирами с баунти и без. В частности, мы выяснили, что два призовых фонда — основной и баунти-фонд — функционируют по-разному:
- Основной призовой фонд (RPP) работает так же, как в обычных турнирах без баунти, и может быть описан с помощью ICM (Independent Chip Model), где каждый стек в фишках преобразуется в денежную эквивалентную стоимость, основываясь на распределении призов.
- Баунти-фонд (BPP), напротив, не зависит от финальных мест игроков и не может моделироваться с помощью ICM. Он описывается моделью Chip EV, которая оценивает будущую ценность фишек, исходя из вероятностей получения оставшихся наград.
Во второй части мы глубже исследуем теоретические последствия того, что оба призовых фонда функционируют как независимо, так и совместно в течение всего баунти-турнира.
Это означает, что любое решение игрока влияет сразу на две ценностные метрики: его долю в RPP и потенциал в BPP. Влияние этих фондов может конфликтовать — или дополнять друг друга.
Основные темы данной статьи будут следующими:
- Как влияние ICM на основной призовой фонд конкурирует с денежной ценностью немедленного выигрыша баунти и увеличением доли игрока в баунти-фонде по мере развития турнира;
- Почему оптимальные стратегии для извлечения максимальной прибыли из общего призового фонда могут значительно отличаться от стратегий, применимых в классических турнирах, в связи с влиянием выигрыша баунти на потенциальную ценность стека при победе в олл-ине с покрытием соперника;
- Как изменяется поведение bubble-фактора в зависимости от соотношения RPP и BPP, и как это влияет на диапазоны пуша и колла;
- Как совместное существование двух моделей (ICM и Chip EV) создает уникальные ситуации, когда ICM-прессинг на стек идет параллельно со стимулированием к агрессии за счет баунти.
ICM, баббл-факторы и просадка эквити (Equity Drops)
На каждом этапе баунти-турнира игрок одновременно испытывает положительное давление риск-премии ICM по отношению к основному призовому фонду и отрицательную просадку эквити (equity drop) — только если он покрывает другого игрока — по отношению к баунти-фонду.
При этом как покрывающий, так и покрываемый игроки также подвержены изменению bubble-факторов из-за их доли в будущем Chip EV баунти-фонда. Это учитывается в формуле bubble-фактора баунти, которая теперь становится двухкомпонентной: одна часть обусловлена ICM, вторая — эквити-рисками, связанными с немедленным получением или упущением баунти.
Сравнение bubble-факторов в разных форматах:
- В стандартном MTT баббл-факторы игроков всегда больше единицы: риск проиграть стек в олл-ине не компенсируется полным эквивалентом выигрыша. Например, баббл-фактор 1.5 означает, что нужно иметь минимум на 10% больше эквити, чтобы оправдать колл.
- В баунти-турнирах все иначе. За счет возможности сразу получить денежное вознаграждение за выбивание, баббл-фактор может быть меньше 1, что означает отрицательную премию за риск.
| Баббл-фактор >1 | Риск-премия |
|---|---|
| 1.25 | +5.5% |
| 1.5 | +10% |
| 1.75 | +13.6% |
| 2 | +16.7% |
| Баббл-фактор =1 | Риск-премия |
|---|---|
| 1 | 0% |
| Баббл-фактор <1 | Риск-премия |
|---|---|
| 0.80 | -5.5% |
| 0.66 | -10% |
| 0.57 | -13.6% |
| 0.50 | -16.7% |
Если bubble-фактор = 1, то риск-премия отсутствует — это ситуация чистого Chip EV, когда фишки эквивалентны денежной стоимости без искажений.
Возьмем ситуацию: игрок на SB пушит, BB коллит. В обычном MTT удвоение почти удваивает $EV. В SKO при этом удваивается и доля в баунти-фонде (моделируемая через ChipEV), плюс мгновенно начисляется фиксированное баунти.
Такой двойной прирост — в фишках и деньгах — и создает условия, при которых баббл-фактор может быть <1, потому что эквити, теряемое в случае поражения, оказывается меньше потенциального выигрыша.
Финальные столы и расчет баббл-факторов
Чтобы на практике увидеть, как изменяется баббл-фактор в разных турнирных форматах, рассмотрим финальную стадию:
Турнир без баунти, бай-ин $100, призовой фонд — $700:
- 1-е место: $400
- 2-е место: $200
- 3-е место: $100
Турнир SKO с бай-ином $50+$50:
- Призовой фонд такой же (тот же основной пул)
- Баунти-фонд: $150 ($50 на выбивание каждого из трёх оставшихся участников)
- Общий оставшийся призовой фонд: $850
Расчеты для турнира без баунти
Пусть короткий стек имеет 15 BB. Его $EV по ICM — около $177. Если он удвоится за счёт среднего стека (25 BB), его $EV возрастёт до ~$246. В случае проигрыша он получит $100. Баббл-фактор:
Средний стек против короткого:
Расчеты для SKO
Для SKO применим аналогичный подход, но с учётом: баунти $50 за выбивание и доли в оставшемся баунти-фонде (расчет по ChipEV).
Средний стек в 25 BB при выбивании игрока в 15 BB получает не только $50 немедленно, но и увеличивает свою долю в оставшемся баунти-фонде (например, с $41.67 до $44.44). Тогда баббл-фактор:
Это эквивалентно премии за риск -5.2%, т.е. у нас отрицательная премия. Если учесть, что в турнире без баунти была +2%, тогда итоговое падение эквити: +2% - 5% = -3%.
Баунти как постоянная и аддитивность эффектов
Ключевой вывод: эквити-падение из-за баунти можно считать статичным, особенно в начале турнира. Оно одинаково для всех покрывающих игроков, и не зависит от размера стека покрытого.
Если бай-ин в SKO — $50+$50, и стек составляет 10,000 фишек, то «стоимость» баунти составляет 5,000 фишек (в пересчете). Тогда в первой раздаче турнира:
- Необходимое эквити на колл = 10,000 / (10,000 + 10,000 + 5,000) = 0.4 = 40%
- Без баунти нам нужно 50% — то есть баунти снижает требуемое эквити на -10%.
Однако в реальных расчетах, например в чартах SKO, падение эквити будет не ровно 10%, а чуть меньше — ~9.5%. Почему? Потому что при выигрыше в олл-ине мы получаем ещё и блайнды, и анте, что немного увеличивает итоговый $EV, и формально уменьшает баббл-фактор.
Объединенное влияние ICM и баунти на стратегию
Из предыдущих расчетов видно, что в баунти-турнирах общее давление на решение игрока определяется суммой двух факторов:
- Положительной премией за риск со стороны основного призового фонда (ICM)
- Отрицательной премией за риск (или падением эквити) со стороны баунти-фонда
Именно это комбинированное давление — и есть итоговая премия за риск, которую мы можем выразить в баббл-факторе. Универсальная формула:
Это объясняет, почему в SKO-турнирах баббл-факторы заметно ниже, чем в обычных: выигрыш баунти создает сильное экономическое давление на решение о колле.
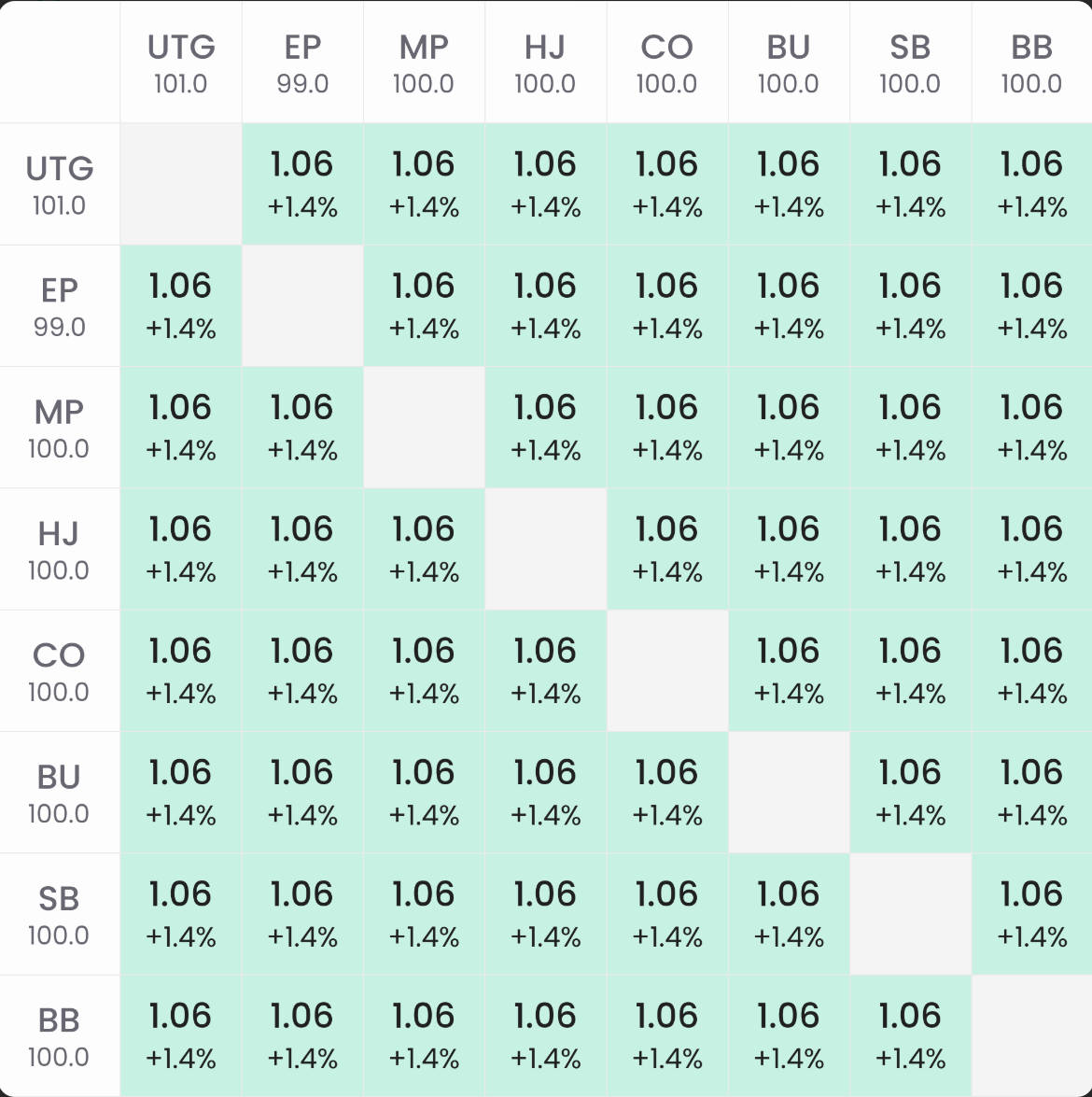
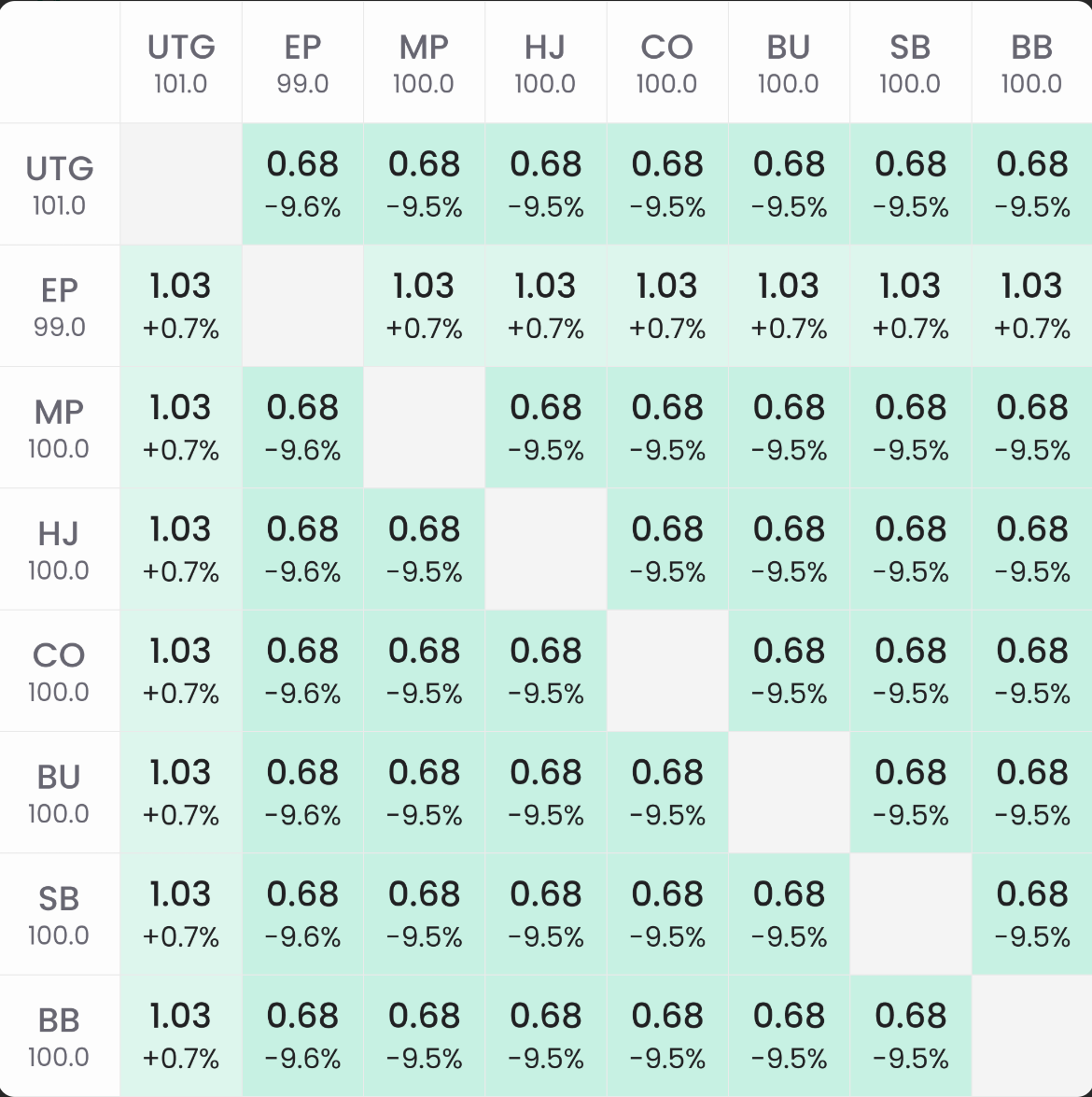
Рассмотрим два MTT с бай-ином $100 и 1,000 участников:
- В первом случае — стандартная ICM-премия: у всех игроков в первой раздаче ~+1.4%.
- Во втором случае: у покрываемых стеков: ~+0.7% (меньше, потому что только половина фонда ICM-чувствительна)
- У покрывающих стеков: ~-9.5%, за счет эквити-падения при участии в олл-ине
В пересчете:
Отклонение можно объяснить техническими нюансами: победитель олл-ина забирает не только стек соперника, но и блайнды + анте. Также возможны округления в финальных значениях баббл-факторов.
Это можно выразить двумя способами: через pot odds — в начале 50% SKO баунти добавляет ~10% к шансу банка, либо через баббл-фактор — сумма положительного давления от ICM и отрицательного (от баунти) дает итоговую премию за риск.
Поэтому, даже если все покрывающие игроки имеют одинаковое $value с баунти, их стратегии могут отличаться в зависимости от текущего распределения стеков — ведь именно это и определяет силу ICM-влияния.
В следующей части, которая будет последней, мы перейдем от теории к прикладному анализу. Речь пойдет о том, как выразить стоимость баунти в фишках и использовать это значение для расчета падения эквити на начальном этапе SKO и PKO-турниров.
Мы также подробно рассмотрим, как правильно конвертировать бай-ин и сумму баунти в «фишечное эквити», и на этой основе — принимать корректные решения в раздачах.
 Покер-румы
Покер-румы