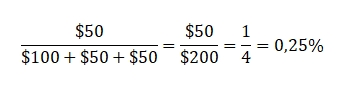Если вы когда-нибудь испытывали трудности с покерной математикой во время раздачи — путались с пропорциями, переводили их в проценты и сомневались в своих решениях — эта статья от авторов подкаста Red Chip Poker покажется вам глотком свежего воздуха.
Они разобрали один из самых распространённых источников путаницы за покерными столами — опору на устаревшую математику, основанную на пропорциях. Традиционный подход к таким вещам, как рассчёт пот-оддсов, имплайд-оддсов или частоты блефа и вэлью зачастую усложняет простые решения и отнимает у вас драгоценные секунды в пылу борьбы.
В этом материале изложен более простой подход: мышление в процентах, отказ от конвертации значений из одной системы в другую и упрощение мыслительного процесса с помощью легко запоминающихся математических шпаргалок. Вы узнаете, как быстрее делать более точные коллы и фолды, отбросив устаревшие инструменты.
Покерная математика: соотношения против процентов
Покеристы склонны использовать математику неоптимальным способом, отчасти потому, что они просто следуют устоявшейся традиции. Например, это относится к расчёту пот-оддсов, имплайд-оддсов и расчёту соотношения блефа и вэлью. И хотя с первыми двумя из этих концепций мы знакомимся в первый же день нашей игры в покер, нам по-прежнему излагают их в устаревшем виде.
Начнём с пот-оддсов. Традиционно они рассчитывались в виде пропорции: например, если в банке $100, и противник поставил полный банк, то наши пот-оддсы на колл составляют 2 к 1 (чтобы выиграть $200, лежащие в банке, нам нужно внести $100). Чтобы понять, устраивает ли нас такая пропорция, мы должны вычислить своё эквити в этом банке и сравнить его с пот-оддсами. Но эквити традиционно вычисляется в процентах, поэтому чтобы сравнить одно с другим, нам нужно перевести пот-оддсы из пропорции в проценты.
Вывод: чтобы облегчить себе жизнь, всегда размышляйте о пот-оддсах как о процентах — это позволяет напрямую сравнивать их с эквити. Если процентное значение эквити выше, чем процентное значение пот-оддсов, то колл выгодный.
Если вы привыкли рассчитывать пот-оддсы в виде пропорции, переучиться будет несложно. В этом вам поможет следующий пример. Представьте, что на тёрне в банке $100, и противник поставил $50. Чтобы перевести наши пот-оддсы в проценты, нужно разделить сумму наших вложений ($50) на финальный размер банка после нашего колла ($100 + $50 + $50), а не до, как в случае с пропорцией:
Если наше эквити выше 25%, значит, мы можем заколлировать с профитом.
Давайте пойдём чуть дальше и зададимся следующим вопросом: каким будет порог безубыточности блефа у оппонента в этом споте? После его ставки на тёрне в банке лежит $150, из которых $50 (33%) составляют саму ставку. Эти 33% и будут порогом безубыточности его блефа — если мы будем фолдить в 33% случаев или чаще, то блеф прибыльный.
Более удобный способ рассчитывать имплайд-оддсы
Перейдём к имплайд-оддсам. С этой концепцией мы знакомимся в самом начале игры в покер, но многие игроки очень быстро её забывают. Они понимают, как имплайд-оддсы рассчитываются в теории, но испытывают трудности с их вычислением по ходу раздачи. Это происходит из-за того, что концепция имплайд-оддсов излагается в неоптимальном виде, что опять-таки является примером плохой математики.
По определению, имплайд-оддсы применяются, когда наши текущие пот-оддсы не могут оправдать колл с дро-рукой. Для этого мы прикидываем, сколько нужно выиграть на будущих улицах, если наше дро закроется, чтобы наш колл с дро-рукой был оправданным. Чтобы упростить этот процесс, мы можем представить размер необходимого банка как множитель к сумме нашего колла. И этот множитель будет статичной величиной в зависимости от типа нашей руки. Например, мы можем установить множитель для флеш-дро, для гатшота и т.д., и эти числа будет легко запомнить.
Вот простой пример. У нас натсовое флеш-дро на тёрне (9 аутов на натс). В банке $100, и противник ставит $50 (те же суммы, что и в предыдущем примере). По «правилу двух» 9 аутов соответствуют вероятности 9×2=18% собрать флеш на ривере, поэтому очевидно, что наших пот-оддсов (25%) недостаточно для колла. Однако это не значит, что в этом споте мы не сможем сделать прибыльный колл, потому что на ривере у нас есть шанс выиграть что-то сверху тех денег, которые сейчас лежат в банке. Но какой должна быть эта сумма?
Чтобы быть оправданным, колл на сумму $50 должен составлять не более 18% от общего банка, на который мы претендуем в этой раздаче, иначе такой колл будет минусовым. Разделив 100% на 18%, мы получим множитель 5,55 (округлим до 6). Умножив это число на сумму нашего колла ($50), мы получим $300 — это и будет минимальный размер окончательного банка, который нам, в среднем, нужно будет выигрывать, когда наше флеш-дро доедет. А поскольку после нашего колла на тёрне банк достигнет размера $200, значит, на ривере нам нужно будет выиграть ещё $100.
Такие вычисления довольно трудно делать в уме во время раздачи — это ещё один пример плохой математики. Более того, половина той работы, которую мы только что проделали, была лишней. Например, зная, что у нас есть 9 аутов, мы перевели их в эквити (18%), а затем вычислили множитель, разделив 100% на 18%. Но 9 аутов на тёрне всегда соответствуют 18% эквити — нет смысла каждый раз тратить на это время, как и на процесс деления для вычисления множителя.
Это значительно упрощает нашу задачу: мы просто умножаем $50 на 6, получаем $300 и видим, что на ривере нам нужно выиграть $300−$200=$100.
Вот таблица для тёрна, по которой можно сопоставить число аутов с множителем нашей ставки:
| Эффективные натсовые ауты | Множитель |
|---|---|
| 4 | 12 |
| 6 | 8 |
| 8 | 6 |
| 9 | 5,5 |
| 10 | 5 |
| 12 | 4 |
| 15 | 3 |
Возможно, и эта таблица будет чрезмерной, поэтому мы можем ограничиться запоминанием множителей только для пяти самых распространённых типов дро-рук, которые являются натсовыми:
| Дро-рука | Множитель |
|---|---|
| Натсовый гатшот (4 аута) | 12 |
| Двухстороннее стрит-дро (8 аутов) | 6 |
| Натсовое флеш-дро (8 аутов*) | 6 |
| Флеш-дро + гатшот (12 аутов) | 4 |
| Двухстороннее стрит-флеш-дро (15 аутов) | 3 |
*На неспаренном борде из 9 аутов на флеш только 8 будут натсовыми, поскольку один из аутов даст пару на столе, и у оппонента будет возможность собрать фулл-хаус или каре.
Для других дро-рук расчёт имплайд-оддсов будет менее актуален. Например, когда мы собрали пару, у нас есть 5 аутов на вторую пару или трипс, но часто такие ауты не будут натсовыми.
Соотношение частоты блефа и вэлью
Соотношение блефа и вэлью при ставке или рейзе — чуть более продвинутая концепция, чем пот-оддсы и имплайд-оддсы, но по традиции она тоже выражается через пропорцию. Но когда мы определяем, нужно ли коллировать ставку оппонента, которая содержит в себе определённое соотношение блефа и вэлью, мы сравниваем это соотношение с ценой колла, которую выше уже договорились вычислять в процентах, как и всё остальное. Как это совместить?
Рассмотрим следующий пример. На ривере противник ставит $50 в банк $100. Здесь перед нами стоят три вопроса:
- Как часто мы должны быть впереди, чтобы колл был плюсовым? Ответом служат наши пот-оддсы: $50/$200=25%.
- Как часто противник должен блефовать в теории? Наши пот-оддсы соответствуют теоретически оптимальной частоте частоте блефа оппонента — это те же 25% (против 75% вэлью-рук).
- Какова наша минимальная частота защиты? Поскольку ставка оппонента автоматически будет прибыльной, если мы будем фолдить в $50/$150=33% случаев или чаще, наша минимальная частота защиты равна 100%−33%=66%.
Подведём итог
Не занимайтесь плохой математикой за покерным столом. В любых покерных расчётах не имеет смысла использовать пропорции — они лишь усложняют работу. Также стремитесь к тому, чтобы не вычислять те числа, которые можно вычислить и запомнить заранее. Это относится не только к множителям для имплайд-оддсов, которые описаны в этой статье, но и к другим вычислениям. Например, если вы рассчитываете свои пот-оддсы каждый раз, когда оппонент ставит 50% банка, вы тоже занимаетесь плохой математикой, поэтому что свои пот-оддсы в этом споте (25%) легко запомнить.
 Покер-румы
Покер-румы